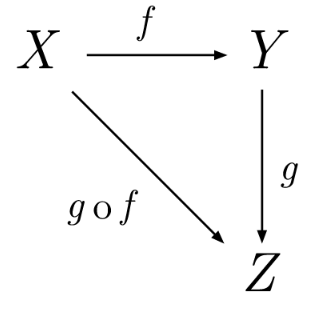book/xq_study/readbook.md

2021/12

函数式编程笔记

• 函数式编程主要解决的问题（通过历史预测未来）

  • 代码复杂度
  • 线程管理
  • 迭代
  • 分布式计算颗粒度

• 编程语言是工具（简化程序复杂度）

  • 软件开发的工具，团队协作软件开发的工具
  • 使用工具到顶了，功能复杂度hold人脑不住了，就要换新工具（人脑几十年的时间不会有什么进化）
  • 应用软件开发：结构化编程 -> 面向对象 -> 函数式编程；可以看到这个路线就是对“状态”的限制使用之路
    
    
    

• 莱布尼兹（与牛顿）曾经有两个梦想：

  • 创建一种“普遍语言”（universal language）使得任何问题都可以用这种语言表述；
  • 对前一个问题的回答就是自弗雷格、罗素开始，经公理集合论运动的最终结果：以一阶谓词逻辑为语言所形式化阐述的集合论，现在已经成为数学的普遍语言，现代逻辑学、特别是将符号逻辑应用于数学领域所产生的数理逻辑，其最重要的目标就是为整个数学提供一个严格精确的语言。这是我们在学习数理逻辑时应当把握的方向。
  • 找到一种"判定方法"（decision method）以解决所有可以在“普遍语言”中所表述的问题
  • 第二个问题则是现代哲学和计算机科学最关注的问题
  • 1928年提出的一个重要的数学问题：“判定性问题” （decision problem），所有计算问题都可以规约到相应的一个判定性问题。“任意正整数是不是素数”这个问题就是可判定的。不可判定问题：“停机问题”、“理发师悖论”-理发师不帮自己理发的人理发，那他该不该帮自己理发？
  • 可计算理论的研究对象有三个 ： ( 1) 判定问题； ( 2) 可计算性；( 3) 计算复杂性（P=？NP）。
  • 1936年，阿隆佐邱奇Alonzo Church 和 阿兰图灵Alan Turing 证明了：为“判定性问题”设计一个通用算法这件事是不可能的。
  • 与此同时，对于“可判定”，他们各自详细阐述了两个计算模型：Alonzo Church的Lambda演算（λ演算），Alan Turing的理论机器（之后被称作图灵机）
  • 
    

• 图灵机

  • 一切可计算的问题都能计算，这样的处理器或者编程语言就叫图灵完备的。
  • Brainfuck （是一种极小化的计算机语言（图灵完备），它是由Urban Müller在1993年创建。

  • Brainfuck 在线编译 https://copy.sh/brainfuck/

    ++++++++++[>+>+++>+++++++>++++++++++<<<<-]>>>++.>+.+++++++..+++.<<++.>+++++++++++++++.>.+++.------.--------.<<+.<.
    

| 字符 | 含义 | | ---- | ------------------------------------------------------------ | | > | 指针加一 | | < | 指针减一 | | + | 指针指向的字节的值加一 | | - | 指针指向的字节的值减一 | | . | 输出指针指向的单元内容（ASCⅡ码） | | , | 输入内容到指针指向的单元（ASCⅡ码） | | [ | 如果指针指向的单元值为零，向后跳转到对应的]指令的次一指令处 | | ] | 如果指针指向的单元值不为零，向前跳转到对应的[指令的次一指令处 |

• Lambda演算（λ）

  • 整个系统是基于表达式的（也叫λ项）:
  • 变量（Variable）：形式：x 变量名可能是一个字符或字符串，它表示一个参数（形参）或者一个值（实参）
  • 抽象体（Abstraction）：    形式：λx.M 它表示获取一个参数x并返回M的lambda函数，M是一个合法lambda表达式，且符号λ和.表示绑定变量x于该函数抽象的函数体M。简单来说就是表示一个形参为x的函数M
  • 应用（Application）    形式：M N 它表示将函数M应用于参数N，其中M、N均为合法lambda表达式。简单来说就是给函数M输入实参N
  • Alpha「转换」（α 转换）: 一个lambda函数抽象在更名绑定变量前后是等价的。λx.x ≡ λy.y

  • Beta「规约」（β-Reduction）：是把标识符用参数值替换；执行任何可以由机器来完成的计算。

    (lambda x . x + 1) 3 == 3 + 1
      
    (lambda y . (lambda x . x + y)) q == lambda x . x + q
      
    (lambda x y. x y) (lambda z . z * z) 3 == (lambda z . z * z) 3 == 3 * 3
      
    //只有在不引起绑定标识符和自由标识符之间的任何冲突的情况下，才可以做Beta规约
    lambda z . (lambda x . x + z)
    (lambda z . (lambda x . x + z)) (x + 2) == (lambda z . (lambda y . y + z)) (x + 2) == (lambda y . y + x + 2) 3 == 3 + x + 2
    

  • 数字：丘奇数都是带有两个参数的函数

  • 0是“ lambda s z . z“

  • 1是“ lambda s z . s z “

  • 2是“ lambda s z . s (s z)

  • x + y

  • let add = lambda s z x y . x s (y s z) == lambda x y . (lambda s z . (x s (y s z)))
    

  • 形如 if / then / else语句的表达式

  • let TRUE = lambda x y . x 
    let FALSE = lambda x y . y 
        
    let IfThenElse = lambda cond true_expr false_expr . cond true_expr false_expr 
        
    let BoolAnd = lambda x y . x y FALSE 
    let BoolOr = lambda x y. x TRUE y 
    let BoolNot = lambda x . x FALSE TRUE 
    

• 图灵机引出了命令式编程

  • FORTRAN（1956 IBM）
  • C（1972 Dennis Ritchie 丹尼斯·里奇）C90 C99
  • C++（1983 贝尔实验室）
  • java （1995 Sun）
  • PHP （1995）
  • C# （2003）

• λ演算引出了函数式编程

  • Lisp（1958） 第二个高级编程语言的，它就是启发自λ演算。
  • Haskell（1985年，Miranda发行，Haskell语言是1990年在编程语言Miranda的基础上标准化的）
  • Python（1991 1994 Python1.0版本发布，这个版本的主要新功能是lambda, map, filter和reduce）
  • Scala（2003 更接近Java习惯，集成了面向对象和函数式编程范式）
  • Clojure（2007 Clojure采用Lisp语法）
  • Groovy（2003 动态类型化，闭包，像java风格的脚本语言，接近Ruby或Python）
  • Kotlin（ 2011 Java 虚拟机，作为 Android 官方支持的第二种编程语言）
  • golang（2009 谷歌）
  • F#（2005）
    

• 函数式编程的语言分类：

  • 只支持函数式范式（如Haskell）
  • 多范式+一流支持（如Scala）
  • 多范式+部分支持（如Javascript、Go）。这类语言中，函数式编程一般通过库来支持，这些库复制前两种语言的标准库中的部分或全部功能。

• 函数式编程的要求：

  • 一等函数/高阶函数
  • 闭包
  • 泛型（go1.18）
  • 尾递归优化
  • 可变个数参数的函数+可变类型参数
  • “柯里化”（Currying）

• 范畴论简介，函数式编程的理论基础;

  • 伴随着范畴论的发展，就发展出一整套函数的运算方法。这套方法起初只用于数学运算，后来有人将它在计算机上实现了，就变成了今天的"函数式编程"。

  • 函数式编程只是范畴论的运算方法

  • 为什么函数式编程要求函数必须是纯的，不能有副作用？因为它是一种数学运算

  • 范畴(category) ；随便什么东西，只要能找出它们之间的关系，就能定义一个"范畴"

  • 

  • 对象/点：object

  • 态射/关系/箭头: morphism, f:a→b

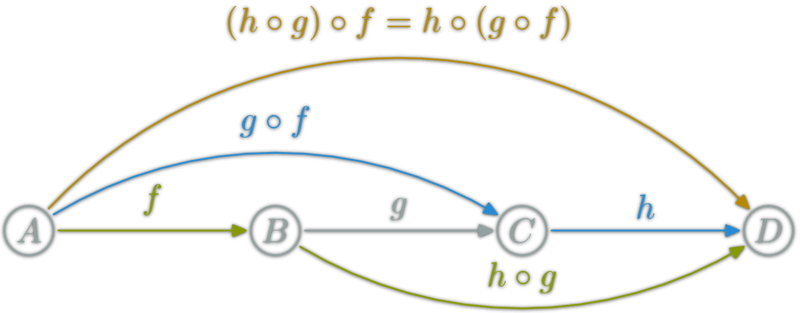
  • 满足结合律：f:a→b,g:b→c 的组合是 g∘f ； 结合律：(h∘g)∘f = h∘(g∘f)

  

  

        const compose = function (f, g) {
          return function (x) {
            return f(g(x));
          };
        }
  

  • 存在恒等态射(identity):

    • 对于任何态射f:a→b，有1b∘f=f=f∘1a ；可以简单的认为是；f(x)=x

  • 柯里化

    • f(x)和g(x)合成为f(g(x))，有一个隐藏的前提，就是f和g都只能接受一个参数。这时就需要函数柯里化了。所谓"柯里化"，就是把一个多参数的函数，转化为单参数函数。

      // 柯里化之前
      function add(x, y) {
      return x + y;
      }
            
      add(1, 2) // 3
            
      // 柯里化之后
      function addX(y) {
      return function (x) {
      return x + y;
      };
      }
            
      addX(2)(1) // 3
      

  • 使用代码，定义一个简单的范畴

    class Category {
    constructor(val) { 
      this.val = val; 
    }
          
    addOne(x) {
      return x + 1;
    }
    }
    

  • 态射的种类：

  • 单态射：不存在两个a中元素 map 到同一个b中的元素。

  • 满态射：每一个b中的元素，都在a中有至少一个 source mapper。

  • 双态射：即是单态射，又是满态射。

  • 同构：a,b两个对象的元素存在一对一的 map 关系。同构 = 双态射 + 存在逆态射。

  • 自态射：表示一个态射源对象和目标对象是同一个, f:a→a

  • 自同构：如果f既是一种自态射，又是具有同构性。

  • 撤回射：如果存在一个f的右逆，其含义是：g 可以通过f找到 source element。f必定是一个满态射

  • 部分射：如果f的左逆是存在的，也就是说，如果存在 g : b→a, g ∘ f = 1a。 f 是另一个态射g的部分射，其含义是：f 确定了g的同构部分。f必定是一个单态射。

  • 同态：是一个态射，表示一个数学结构A到另一个数学结构B的map关系，并且维持了数学结构上的的每一种操作*。  f:A→B，有： f(x∗y)=f(x)∗f(y)

    • 同一种操作在不同的数学结构上定义可以不同。
    • 比如：指数函数是一个同态。e(x+y)=exey→f(x∗y)=f(x)∗f(y)

  • 函子(functor)

  • 函子是函数式编程里面最重要的，也是基本的运算单位和功能单位。

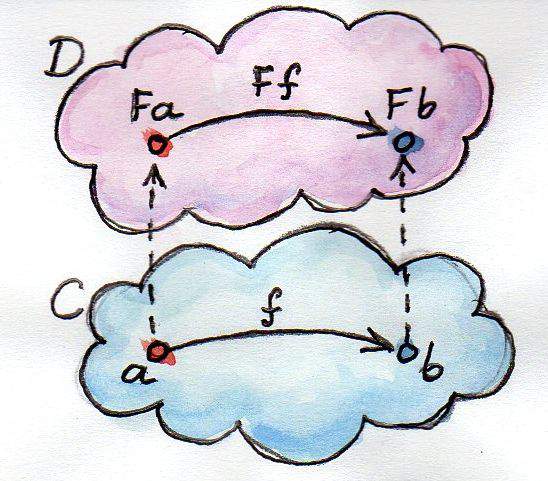
  • 函子是范畴之间的map关系。可以理解为范畴之间的态射。

  • 图中，函数f完成值的转换（a到b），将它传入函子，就可以实现范畴的转换（Fa到Fb）。

  • 

  • 具有map方法的数据结构，都可以当作函子的实现。代码中，Functor是一个函子，它的map方法接受函数f作为参数，然后返回一个新的函子，里面包含的值是被f处理过的（f(this.val)）。

  • class Functor {
    constructor(val) { 
      this.val = val; 
    }
          
    map(f) {
      return new Functor(f(this.val));
    }
    }
    

  • 函数式编程里面的运算，都是通过函子完成，即运算不直接针对值，而是针对这个值的容器----函子。函子本身具有对外接口（map方法），各种函数就是运算符，通过接口接入容器，引发容器里面的值的变形。因此，学习函数式编程，实际上就是学习函子的各种运算。由于可以把运算方法封装在函子里面，所以又衍生出各种不同类型的函子，有多少种运算，就有多少种函子。函数式编程就变成了运用不同的函子，解决实际问题。

  • Maybe 函子

  • Either 函子(运算if...else)

  • ap函子，函子里面包含的值，完全可能是函数。我们可以想象这样一种情况，一个函子的值是数值，另一个函子的值是函数。

  • 协变函子 F:C→D

    • 对于每一个 C 中的对象x，对应一个 D 中的F(x)。
    • 对于每一个C中的态射f:x→y，对应D的态射F(f):F(x)→F(y)。

  • 逆变函子

    • 和协变函子类似，只不过态射的方向是从D到C。

  • 自然转换(Natural transformation)

  • 自然转换是两个函子之间的关系。函子描述“自然构造(natural constructions)”，自然转换描述两个这样构造的"自然同态(natural homomorphisms)"。

  • Map-Reduce-Filter 模式（高阶函数）

  • reduce

  • //在Haskell中是没有循环的，由于循环能够经过递归实现，在咱们实现的sum函数中，也没有用到任何循环语句，这和咱们原来的编程思惟有所不一样，刚开始写求和函数的时候，都是从for,while开始的，可是函数式给我打开了新世界的大门。
    //递归 尾递归
    func foldr(f func(a,b int) int,z int,list []int)int{
    if len(list) == 0{
        return z
    }
    return f(list[0],foldr(f,z,list[1:]))
    }
        
    func add(a,b int) int{
    return a+b;
    }
        
    func sum(list []int) int{
    return foldr(add,0,list)
    }
        
    func main(){
    a := []int{1,2,3}
    sum(a) // 6
    }
    

  • //复用 foldr 高阶函数
    func muti(a,b int) int{
    return a*b;
    }
        
    func product(list []int) int{
    return foldr(muti,1,list)
    }
    

  • function flip(f, a, b){
     return f(b,a);
    }
    //这个函数须要进行柯里化，不然没法在foldr中做为参数传入
    var flip_ = _.curry(flip);
        
    function cons(a,b){
     return a.concat(b);
    }
        
    function reverse(list){
    return foldr(flip_(cons),[],list);
    }
        
    console.log(reverse([1,2,3]))
    // [ 3, 2, 1 ]
        
    //curry，柯里化。简单地说，柯里化就是一个函数能够先接受一部分参数，而后返回一个接受剩下参数的函数。用上面的例子来讲，flip函数在被柯里化以后获得的函数flip_，能够先接受第一个参数cons而后返回一个接受两个参数a,b的函数，也就是咱们须要的链接函数。
        
    //在go语言里面，实现curry，可用用第三方包。
    

  • //先定义一个count函数
    function count(a,n){
    return n + 1;
    }
    //再实现length函数
    function length(list){
    return foldr(count,0,list);
    }
    //调用
    console.log(length([1,2,3,4]));
    // 4
    

  • reduce咱们讲完了，而后咱们看看map

  • //go 的尴尬之处在于，须要很是明确的函数定义，因此咱们要从新写一个foldr函数，来接受第二个参数为列表的f
    func foldr2(f func(a int,b []int) []int,z []int,list []int)[]int{
    if len(list) == 0{
        return z
    }
    return f(list[0],foldr2(f,z,list[1:]))
    }
        
    func doubleandcons(n int,list []int) []int{
    return append([]int{n * 2},list...)
    }
        
    func doubleall(list []int) []int{
    return foldr2(doubleandcons,make([]int,0),list)
    }
    // doubleall([]int{1,2,3,4})
    //[2 4 6 8]
    

  • function fandcons(f, el, list){
    return [f(el)].concat(list);
    }
    //须要柯里化
    var fandcons_ = _.curry(fandcons);
        
    function map(f, list){
    return foldr(fandcons_(f),[],list);
    }
    //调用
    console.log(map(function(x){return 2*x},[1,2,3,4]));
    // 输出[ 2, 4, 6, 8 ]
    

  • -- map的一些神奇的操做：矩阵求和
    summatrix :: Num a => [[a]] -> a
    summatrix x = sum (map sum x)
        
    -- 调用
    summatrix [[1,2,3],[4,5,6]]
    -- 21
    

  • function sum(list){
    return foldr(add,0,list);
    }
    function summatrix(matrix){
    return sum(map(sum,matrix));
    }
    //调用
    mat = [[1,2,3],[4,5,6]];
    console.log(summatrix(mat));
    //输出 21
    

  • filter

  ---

  2021/5

  笔记

  • 历史

  • 实体机以前，先有理论（指令集有了，可以编程了）

  • 可计算问题，整数可以表示所有可计算问题

  • 图灵机

  • λ演算

  • 图灵完备的指令集，解决了机器的问题，剩下的主方向是人的问题

  • 人如何在这个完全人造的指令集上创造世界--程序设计--软件工程

  • 自上而下的规划设计，自下而上的进化体系

  • 软件设计是很复杂的全人造世界，几十年的发展不足以使它成熟

  • 软件设计不仅要了解事物运作的本质关系，同时也是创造一个世界

  • 真实世界是怎么被创造的呢？不是规划是进化的。生物的进化，计划经济到市场经济的转变，unix系统进化

  • 简单的基本单位或概念（细胞，经济个体，文件），简单的规则（经济规律，文本化通信规则）

  • 软件设计所需要的能力（抽象能力，洞察力）

  • 软件危机

  • 软件复杂性，复杂性四个原因：

  • 问题域的复杂性；（大型系统，需求沟通，需求变化）

  • 管理开发过程的困难性；（数百数千的独立模块，团队开发成员复杂的沟通，特别是远程协作开发）

  • 通过软件可能实现的灵活性；（软件开发领域是不成熟的，缺少成熟稳定的标准，软件灵活性能做各种事，这是很诱人的）

  • 刻画离散系统行为（大型应用中，大量的变量状态，多个控制线程，构成系统的了离散状态；系统状态的转换是非确定性的，我们的只能不足以对大型离散状态系统进行完整性的建模，完整新是指穷尽所有状态）

  • 克服人类能力的限制

  • 处理复杂性时人的智力的局限性（一个人能够同时处理的最大信息数量是7个，上下浮动2个，这于短期记忆能力有关）

  • 抽象的意义

    • 抽象是人类处理复杂性的基本方式（人类区别于动物的特征）
    • 命名（最基本的抽象方法），可变（内容可变）
    • 计算过程抽象
    • 数据抽象
    • 分层（互联网7层协议）（很容易维护和修改）

  • 类型的意义

    • 表达抽象概念

  • 封装的意义

    • 要让抽象能工作，就要将其封装起来（分离接口和实现）

  • 模块化的意义

    • 模块化构造了良好的程序边界（对于大型程序管理复杂性很有益）

  • 紧凑型和正交性（复杂度是否能装入人脑；操作的不相关性，修改每个属性的方法有且只有一个）

  • 并发的意义

    • 多处理器
    • 功能独立的模块（GUI和计算逻辑）（隔离）
    • 多资源（多I/O设备）
      

  • 复杂软件系统设计的要素

  • 表示法（编程语言，影响复杂度）（表现力，阿拉伯数字表示法）

  • 设计过程（分解；抽象；层次结构）

  • 工具（IDE，log ，性能分析，编码格式规范，代码管理，单元测试等等）

  • 编程语言历史，随着硬件能力的增长

  • 从小规模编程向大规模系统转变

  • 编程语言的演进和分类

  • 机器码 - 汇编语言 - 高级语言（编译语言，解释型语言；编译时/运行时，强类型/弱类型） - 框架

  • 高级语言（数学表达式 - 算法抽象，子程序 - 数据抽象 - 面向对象- 函数式编程- 逻辑式语言）

  • 脚本语言（按着使用场景，通常是解释型）

  • 命名和绑定（一切抽象的起始）

  • 给一个东西命名（变量、常量、类型、子程序、模块等等）

  • 名字代表的东西可变化（变量和赋值）

  • 绑定（赋值）：一个东西和一个助记符建立联系（建立联系的时间，编译时/运行时）

  • 一个东西创建到销毁是对象的生命周期（分配内存）

  • 一个东西于助记符绑定的建立到撤销是绑定关系的生命周期

  • 静态分配内存

  • 早期高级语言只有静态分配（子程序内部的变量也是静态分配的）

  • 动态分配内存（有分配有回收）

  • 基于栈的分配（用于函数调用，造成了局部变量，从而支持递归）

  • 栈结构（进程栈，线程栈，内核栈，中断栈）函数调用/多任务调度

  • 递归（同一个子程序存在多个实例）

  • 基于堆的分配 new（创建和销毁由程序员控制）

  • 数组、类的实例、字符串等需要大块存储区域的数据结构

  • 对分配策略（速度于空间平衡）

  • 垃圾回收（自动化回收堆空间）

  • 作用域规则

  • 作用域（声明语句所在的代码块 表明作用域）

  • 引用环境（当去运行当前能够访问到的所有名字绑定关系的集合构成当前的引用环境）

  • 静态作用域（编译时确定）（大多数现代语言）

  • 嵌套子程序中作用域

  • 声明引进的名字在这个声明所在的区域可见，以及其内部所嵌套的每个子作用域中可见，除非因为同名而被屏蔽掉（子程序内部访问它的父程序的绑定关系，这个绑定关系不在本子程序的栈帧中，需要一种记录机制）

  • 一些语言把某个嵌套子程序的“引用环境”关联起来或者保存起来，结果就是产生了”闭包“

  • 动态作用域

  • “引用环境”是动态更新的，带来很大的灵活性，比如动态的切换子程序执行的引用环境；

  • 解释型语言

  • 一级状态（一等公民）

  • 一个值可以赋值给变量、可以当作参数传递、可以从子程序返回，那么它被称为具有一级状态

  • 在具有嵌套作用域的语言中，一级子程序会带来复杂性（闭包的“引用环境”，不能在栈，而在堆，限一些语言制嵌套子程序的使用）

  • 一个对象可以有多个名字（别名），一个名字也可以代表多个对象（重载）

  • 函数重载带来的还有两个常见的特性，多态性和强制类型转换；在面向对象语言中，会有继承的子类型的多态性以及强制转换，比如一个接受接口类型参数的方法，可以通过传递一个子类类型来调用。还有一种多态称之为类型化参数的多态性（通常我们称之为“泛型”）

  • 控制流

  • 顺序执行，选择，迭代，过程抽象，递归，并发，无顺序

  • 命令式语言中视顺序执行为核心；函数式语言中则大量使用递归；逻辑式语言则有意的模糊控制流这种东西。

  • 表达式求值

  • 运算符（内置函数）

  • 运算符和运算对象的组合就是表达式（前缀、中缀和后缀表达式）

  • 大部分语言都会区分表达式和语句（赋值），前者产生一个值，或许会有副作用；而后者的执行就是为了产生副作用（修改状态）

  • 赋值：值模型，引用模型

  • 多路赋值：a,b=b,a;

  • 表达式里的顺序问题，大多数语言并未明确规定求值顺序 p = (a++)+(a++)*5/3;

  • 结构化和非结构化的流程

  • 汇编语言中的控制流通过有条件的或无条件的跳转指令来完成

  • 早期的高级语言模仿这种方式，主要依赖goto

  • 后续高级语言中已经禁止了goto或者仅仅在受限的上下文环境中使用。在结构化的程序中，一个子程序中的流程控制都可以通过顺序、选择、迭代、递归来描述，结构化语言不依赖标签，而是词法上嵌套的词法边界作为流程控制的结构单元。

  • 架构化语言封装运算过程（无限制的goto打破封装）

  • goto的结构化代替品 break，contiune，return，局部goto

  • 迭代和递归

  • 命令式语言中，迭代显得更自然一些，因为它们的核心就是反复修改一些变量；对于函数式语言，递归更自然一些，因为它们并不修改变量

  • 尾递归函数是指在递归调用之后再无其他计算的函数，其返回值就是递归调用的返回值。对这种函数完全不必要进行动态的栈分配，编译器在做递归调用时可以重复使用当前的栈空间（通常编译器自动做优化）

  • 应用序和正则序求值

  • 所有参数在传入子程序之前已经完成了求值，但是实际中这并不是必须的。完全可以采用另外一种方式，把为求值的之际参数传递给子程序，仅在需要某个值得时候再去求它。前一种在调用前求值的方案称为应用序求值；后一种到用时方求值的方式称为正则序求值。

  • 正则序求值可能引起副作用（在函数式编程中无副作用）

  • 数据类型（bit + 上下文 == 信息）

  • 上下文：类型提供了隐含的上下文信息，使程序员可以在许多情况下不必显示的描述这种上下文

  • 类型描述了其对象上一些合法的可以执行的操作集合；编译器可以使用这个合法的集合进行错误检查，如在编译阶段强制检查的语言大部分都是强类型语言、在运行时检查的大都是弱类型语言。

  • 类型系统

  • 汇编语言无类型

  • 类型对于编程来说是一种抽象封装，用于上下文信息和错误检测

  • 类型等价规则：确定两个值得类型何时相同

  • 类型相容规则：确定特定类型的值是否可以用在特定的上下文环境里（禁止把任何操作应用到不支持这种操作的类型对象上的规则）

  • 类型推理规则：基于一个表达式的各部分组成部分的类型以及其外围上下文来确定这个表达式的类型

  • 一些语言中，子程序也是有类型的（参数的个数和类型来确定子程序的类型）

  • 类型检查：保证程序遵循了语言的类型相容规则；严格的类型检查会使编译器更早的发现一些程序上的错误，但是也会损失一部分灵活性

  • 多态性使得同一段代码体可以对多个类型的对象工作。它意味着可能需要运行时的动态检查，但也未必一定需要（类型推理系统）：面向对象语言里，子类型多态；显示的参数化类型（泛型）

  • 类型等价：

  • 结构等价

  • 名字等价（现代编程语言大都基于名字等价）

  • 通用类型：java的Object ，C中的void*，go 的 interface{}

  • 数组

  • C#和Java里的数组变量是对象（面向对象语言中所指的对象）的引用

  • go 数组变量保存的是一个结构体，结构体里有指针和其他数组其他信息

  • 大多数语言的实现里，一个数组都存放在内存的一批连续地址中

  • 字符串

  • 指针

  • 在一些语言中，指针被严格的限制为只能指向堆里的对象 new

  • 另一些语言中，可以用“取地址”操作创建指向非堆对象的指针

  • 值模型，引用模型

  • Java的实现方式区分了内部类型和用户定义的类型，对内部类型采用值模型，对用户定义的类型采用则采用引用模型

  • go 可以理解为全是值模型，指针也是一种值

  • 面向对象特征（认为事物的关系 is a ， has a）（对象之间不共享的状态远大于共享状态时，面向对象编程比较好）

  • 支持对象

  • 类型

  • 继承

  • 函数式编程特征

  • 函数是一等的（函数可以作为参数和返回值）

  • 纯函数，无状态

  • 数据驱动编程的核心是数据结构（建模），而不是算法

  • 数据驱动是一种思想，从数据出发思考（例如：常见的表驱动法）

  • 元语言抽象（创造一种新语言，逻辑式语言，SQL，正则表达式）

  • 将基本元素组合起来，从复合元素出发，过程抽象

  • 编程的本质就是控制复杂度

  • 过程化编程 - 面向对象编程 - 函数式编程 - 逻辑式编程

  • unix文化

  • 很多小工具命令，数据流使用统一的文本化（统一信息格式），使用管道连接起来，也可以使用shell脚本调用

  • KISS ： keep it simple stupid

  • 一切皆文件（细胞）

  • 开源文化：linux apache mysql 。。。（unix历史的教训，距离开源越近越繁荣）

  • 作为编程语言，创造世界的工具，go语言一些特点（助于我们学习和使用go语言）

  • 所有变量传递都是值传递，没有引用的语法概念，指针类型也是保存的一个值

  • 接口的使用

  • go是面向对象语言么

  • go是函数式编程语言么

  • go自己的编程范式

  • 并发方案（goroutine 和通道）

  • 虚拟机与运行时环境（goroutine调度器，垃圾回收）

  • 各种工具集成到go语言编译环境内（编码格式，性能分析，包管理，测试。。。）

  • 栈，堆和变量逃逸

  • 80年代c；为什么是java；为什么是go（主流工业级系统开发基本没有小型系统了；编程语言作为被选型的用来描述和创造虚拟世界的工具）

  • 推荐书：

  • 计算机程序的构造和解释，

  • 程序设计语言实践之路，

  • Unix编程艺术，

  • 深入理解计算机系统